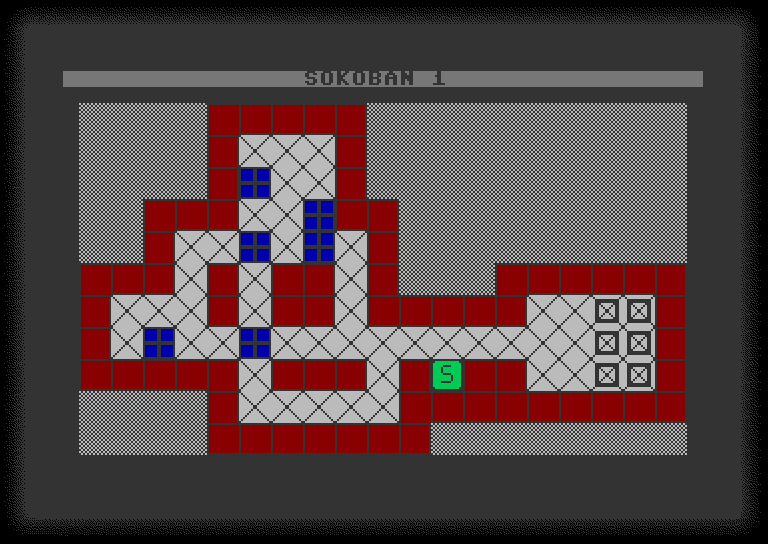
Ein Besuch auf der Seite mathematik.ch vor einiger Zeit hat mich daran erinnert, wie gern ich vor vielen Jahren einmal das Denkspiel Sokoban gespielt habe. Es hat mich sofort wieder in den Bann gezogen. Da lag die Idee nicht fern, ob man ein solches, nach einfachen Regeln funktionierendes Spiel nicht auch selber programmieren könnte. TSB sollte doch alle erforderlichen Möglichkeiten zur Verfügung stellen.
Was braucht man an Material? Zeichensatzumstellung (geht: mit MEM), Cursor-Positionierung (geht: mit PRINT AT) und was noch? Ein bisschen "Gebimmel" hier und da, wenn etwas Besonderes passiert (geht auch: mit BFLASH z.B.) und das wär's dann schon.
Was brauchen wir noch? Einen Plan für die Spielmechanik.

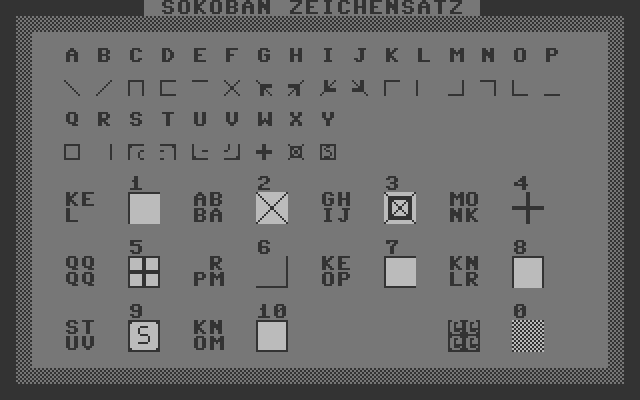
Erstens: Das Spielfeld muss aufgebaut werden, es besteht aus verschiedenen unbeweglichen Rand- und Hindernissteinen und aus zwei beweglichen Spielfiguren, dem Sokoban einerseits und den "Kisten", die er hin- und herschieben soll, andererseits. Schließlich brauchen wir noch die Markierungen für die Ablagefelder, wo die Kisten hingeschoben werden sollen. Die erforderlichen Zeichen dafür kann man mit TSB schnell erzeugen (mit DESIGN 2, Tipps dazu hier). Der erste Versuch ist hier im Bild zu sehen: Jeder Feldstein ist darin ein Zeichen groß. Aber: Das ist zu klein, man muss sich beim Hinschauen anstrengen. Daher gehen wir besser auf 2×2-Kacheln über (Bild ganz oben auf dieser Seite). Wir brauchen elf verschiedene, um ein Spielfeld darzustellen:
Zweitens: Der Sokoban kann seine Kisten nur in eine Richtung schieben, nämlich vorwärts. An Hindernissen geht es für die beweglichen Figuren nicht weiter. Er bewegt sich also auf den freien Parkettkacheln in vier Richtungen: vorwärts, rückwärts, links oder rechts. Diagonal oder springen geht nicht, die Spielfiguren müssen dem Feldraster folgen. Das ist ein Grund, auf Sprites zu verzichten, der Sokoban und die Kisten sollen definitiv aus Zeichen bestehen.
Das bedeutet, dass wir beim Bewegen einer Figur drei Dinge tun müssen: 1. Checken: Ist die Zielkachel betretbar? 2. Ja, ersetze die Zielkachel durch die Spielfigur. 3. Rekonstruiere die Kachel, auf dem die Spielfigur eben noch stand. Bewegt sich nur der Sokoban, muss man also zwei Kacheln im Auge behalten. Bewegt sich der Sokoban zusammen mit einer Kiste, sind es drei Kacheln.
Und damit sind wir bei programmtechnischen Überlegungen angelangt: Wie repräsentieren wir ein Spielfeld? Wie überwachen wir Bewegung und Aktionen? Spielfelder muss man sich als eine Matrix aus Einzelzellen (Kacheln) vorstellen, so wie etwa ein Schachbrett: x Zellen breit, y Zellen hoch. In Basic sind Arrays wie gemacht für diesen Zweck. Jede der Zellen erhält Informationen über ihre Aufgabe im Spiel zugewiesen: Du bist ein Hindernis, du bist eine Ablagezelle, du bist eine Kiste, du bist der Sokoban usw. Für eine Bewegung müssen zuerst die Nachbarzellen überprüft werden: Darf ich drauf (ja, wenn es eine Parkettzelle ist), ist eine Kiste drauf (wenn ja, darf die Kiste auf die übernächste Zelle rutschen)? Schauen wir genauer hin.
90 if display=$0400 then mem: cset1: print "wait...": load "sokoban.chr",0,0,$ec00
100 cls: check: init
110 loop: exit if x$="x"
120 setzen: end loop
999 end
5500 proc init
5520 print"{rvs on}";: fb=11:fs=5:f0=15:f1=2:f2=15:f3=15:f4=6:f5=6:f6=2:f7=2:f8=2:fa=2
5530 colour 12,fb,12:read n:dim fd%(n)
5535 for i=1 to n:read fd%(i):next
5540 if peek(2)>0 then p=peek(2):if p>n then finale:end proc
5550 if fd%(p)=0 then p=p+1:poke2,p
5560 reset fd%(p)
5570 pk=0:al=0:in=0:read p,b,h,sy,sx:dim f%(b,h),g%(b,h)
5575 oy=0:if h=12 then oy=1
5580 ox=1:if b=20 then ox=0
5585 z=2-oy:s=ox
5590 fill 0,0,40,25,224,fb
5592 feld
5595 end proc
6000 data 10,6005,6120,6230,6340,6460,6590,6720,6850,6970,7090
6005 data 1,19,11,9,12
Die Zeilen 90 bis 999 stellen das Hauptprogramm dar. Hier wird initialisiert (Z. 90/100) und gespielt (Z. 110/120). Das ist dann schon alles.
Na ja, nicht ganz. In der INIT-Prozedur legen wir zunächst alle Farben fest (die F-Variablen, jedes Objekt von 0 bis 10 erhält seine individuelle Farbe, FS ist der Sokoban, FB die Background-Farbe, Zeile 5520). In Z. 5530/5535 erfassen wir, wie viele Sokoban-Spielfelder das Programm bietet (N) und an welchen Stellen im Programm sie sich befinden (die entsprechenden Basic-Zeilennummern werden nach FD%() eingelesen aus Z. 6000).
Da ein neues Spielfeld der Einfachheit halber immer mit RUN gestartet wird, übergeben wir die laufende Nummer des Spielfelds an einer Speicherstelle, die von Basic bei RUN nicht beeinflusst wird: $0002 (Z. 5540/5550). Danach lesen wir die Daten für dieses Spielfeld ein (Z. 5560/5570), im Beispiel für Spielfeld 1 in Zeile 6005. Dort steht die Nummer, die in der Überschrift angezeigt wird (hier: 1), Breite und Höhe des Feldes (hier: 19 und 11) und das Startfeld des Sokoban (Zeile und Spalte im Spielfeld, hier 9 und 12). Da ich mir erlaubt habe, kleinere Spielfelder etwas einzurücken, müssen dafür in den Zeilen 5575/5580 Ausgleichsvariablen her, wenn Spielfelder in Maximalgröße vorkommen (OX und OY). Zeile 5585 legt in Z (Zeile) und S (Spalte) die linke obere Ecke des Spielfeldes fest. Dann wird in den Zeilen 5590 und 5592 das Spielfeld aufgebaut.
Wer genau hingesehen hat (was wir ja wollten), hat gemerkt, dass das Spielfeld-Array zweimal angelegt wird (Z. 5570). Warum das denn?
Einfache Antwort: Im Klon-Array g%() lassen wir die beweglichen Objekte weg. Wenn wir uns später im Spielfeld bewegen, haben wir hiermit eine sichere Quelle darüber, was sich im Feld, auf dem man steht, vorher befunden hat (das spielt bei den Ablagefeldern eine Rolle). Außerdem können wir durch Vergleich der beiden Arrays schnell feststellen, ob die Ablagefelder vollständig mit Kisten besetzt sind, das Spiel also erfolgreich abgeschlossen wurde.
Aufbau des Spielfeldes
3000 proc feld 3010 print at(0,0) dup(chr$(160),40); 3020 print at(0,0)"";: centre"SOKOBAN"+str$(p) 3025 pk=0: for i=1 to h: for j=1 to b: readx: f%(j,i)=x:g%(j,i)=x 3030 if x=0 then k0 3035 if x=1 then k1 3040 if x=2 then k2 3050 if x=3 then k3 3060 if x=4 then k4 3070 if x=5 then k5:g%(j,i)=2:pk=pk+1 3075 if x=$88 then k5:g%(j,i)=3:f%(j,i)=5:pk=pk+1 3080 if x=6 then k6 3090 if x=7 then k7 3100 if x=8 then k8 3110 if x=9 then k9:f%(j,i)=2:g%(j,i)=2 3112 if x=12 then k9:f%(j,i)=3:g%(j,i)=3 3115 if x=10then ka 3120 s=s+2: next: s=ox:z=z+2: next: z=sy*2-oy:s=(sx-1)*2+ox 3130 end proc 6010 data 0,0,0,0,1,7,7,7,8,0,0,0,0,0,0,0,0,0,0 6020 data 0,0,0,0,8,2,2,2,8,0,0,0,0,0,0,0,0,0,0 6030 data 0,0,0,0,8,5,2,2,8,0,0,0,0,0,0,0,0,0,0 6040 data 0,0,1,7,10,2,2,5,7,8,0,0,0,0,0,0,0,0,0 6050 data 0,0,8,2,2,5,2,5,2,8,0,0,0,0,0,0,0,0,0 6060 data 1,7,10,2,8,2,1,8,2,8,0,0,0,1,7,7,7,7,8 6070 data 8,2,2,2,10,2,7,10,2,7,7,7,7,10,2,2,3,3,8 6080 data 8,2,5,2,2,5,2,2,2,2,2,2,2,2,2,2,3,3,8 6090 data 7,7,7,7,8,2,7,7,10,2,8,9,1,8,2,2,3,3,8 6100 data 0,0,0,0,8,2,2,2,2,2,1,7,7,7,7,7,7,7,10 6110 data 0,0,0,0,7,7,7,7,7,7,10,0,0,0,0,0,0,0,0
In den DATAs liegen die ID-Nummern der Objekte, wie sie im Bild "SOKOBAN ZEICHENSATZ" weiter oben auf dieser Seite zu sehen sind: 11 DATA-Zeilen mit je 19 IDs. Sie werden in den Zeilen 3025 bis 3120 in sichtbare Objekte verwandelt (zu den Zeilen 3075 und 3112 später mehr). In den Zeilen 3070 und 3110 löschen wir im Klon-Array g%() die beweglichen Teile weg und zählen mit PK die zu bewegenden Kisten. Zuletzt wird die Startposition des Sokoban in Koordinaten auf dem Bildschirm umgerechnet (in den Variablen Z und S, Z. 3120). Da dies die aktuelle Position für alle weiteren Bewegungen ist, wird die zugehörige ID (ID 9) nicht im Array eingetragen, der Sokoban ist ab jetzt ein "Geist", die ID 9 kommt in den Arrays nicht mehr vor. Alle folgende Objektpositionierung geschieht nun über die beiden Variablen Z und S. Das sieht so aus (Beispiel Objekt-ID 9: "Sokoban"):
4270 proc k9 4280 colour,fs: print at(z,s)"st" at(z+1,s)"uv"; 4290 end proc
Bewegung des Sokoban
Vorab: In der Prozedur "setzen" können wir - neben der Bewegung der Figuren - mit den Tasten "X", "N" und "R" den weiteren Spielverlauf beeinflussen. "R" (für Restart) stellt das aktuelle Spielfeld auf die Anfangsposition zurück (wenn man sich festgefahren hat), "N" wechselt sofort zum nächsten Sokoban-Problem und "X" ist die Keine-Lust-mehr-Taste (Z. 3980 bis 3990).
3900 proc setzen
3910 repeat: get x$
3920 if x$="{crsr up}" then auf
3930 if x$="{crsr dwn}" then ab
3940 if x$="{crsr lft}" then nl
3950 if x$="{crsr rgt}" then nr
3955 if in>=pk then ablage: if in>al then in=al
3965 if al=pk then x$="x": finish
3980 until place(x$,"xnr")
3985 if x$="r" then run
3990 if x$="n" then p=peek(2): p=p+1: poke2,p: run
3995 end proc
3915 x=joy(2) and 127: if x then x$=mid$("{crsr up} {crsr rgt} {crsr dwn} {crsrs lft} ",x,1).
Der Sokoban wird mit den Cursor-Tasten bewegt (Zeilen 3920 bis 3950, s. aber auch die Anmerkung). Bei jeder Bewegung muss überprüft werden, ob sie zulässig ist. Das Feld, in das man hineinwill, darf kein Rand- oder Hindernisfeld sein. Im Prinzip ganz einfach, man schaut nach, ob in der Array-Zelle, die zum anvisierten Feld gehört, eine entsprechende ID steht (ID 2 für Parkett). Ist das der Fall, kann die Bewegung durchgeführt werden. Der Sokoban (ID 9) wechselt also ins anvisierte Feld (k9) und rekonstruiert danach das Feld, von dem er kam (k2). Für die Aufwärtsbewegung macht das die Prozedur "auf":
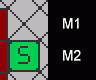
3200 proc auf 3210 z=z-2: i=z/2+oy: j=s/2+1: m1=f%(j,i): m2=f%(j,i+1) 3215 if m1=5 then pauf 3217 if m1=2 then if m2=3 then k9: z=z+2: k3: z=z-2: end proc 3220 if m1=2 then k9: z=z+2: k2: z=z-2: end proc 3230 if m1=3 then if m2=3 then k9: z=z+2: k3: z=z-2: end proc 3235 if m1=3 then if m2=2 then k9: z=z+2: k2: z=z-2: end proc 3240 if m1<>2 then z=z+2: k9 3245 end proc
Mit z=z-2 visieren wir das Feld oberhalb des Sokoban an. Zeile und Spalte werden umgerechnet auf die entsprechenden Array-Positionen und der Inhalt des Arrays dort in den Variablen M1 (Ziel) und M2 (Standort) festgehalten (alles in Z. 3210). Ist in M1 eine 2 (Parkett) dann wird dort der Sokoban ausgegeben (k9), die Zeile unterhalb anvisiert (z=z+2), das Parkett ausgegeben (k2) und mit einem abschließenden z=z-2 wieder auf die Zeile oberhalb gewechselt, weil das jetzt der neue Standort des Sokoban ist (Z. 3220).
Die weiteren Basic-Zeilen in der Prozedur brauchen wir nun, weil der Sokoban auch über Ablagefelder (ID 3) marschieren kann. Und da können mehrere Situationen auftreten: der Sokoban ist auf einem Parkettfeld (M2=2) und will die Ablage (M1=3) betreten (Z. 3235), Sokoban ist in der Ablage (M2=3) und das Zielfeld ist auch dort (M1=3, Z. 3230), Sokoban ist in der Ablage (M2=3) und verlässt sie mit dem nächsten Schritt (M1=2, Z. 3217).
Falls jedoch im Zielfeld eine Kiste (ID 5) stehen sollte (M1=5 in Z. 3215), dann erfolgt eine Sonderbehandlung (siehe nächster Abschnitt). Alle anderen Inhalte von M1 (M1<>2) sagen, dass wir vor einem Hindernis stehen und nicht in diese Richtung weitergehen dürfen (Z. 3240).
Für die anderen drei Richtungen (nach rechts mit PROC nr, nach links mit PROC nl und nach unten mit PROC ab) gilt die gleiche Vorgehensweise.
Bewegung der Kisten
Steht der Sokoban vor einer Kiste (ID 5) und bewegt sich vorwärts, nimmt er die Kiste mit, sofern ihn nichts daran hindert. Wir müssen also das Feld jenseits der Kiste überprüfen. Im Programm erhält es die Bezeichnung M3.
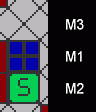
3400 proc pauf 3405 m3=f%(j,i-1) 3410 if m3=2 then z=z+2:k2: mauf: if m2=3 then z=z+4: k3: z=z-4 3412 if m3=3 then if g%(j,i)=2 then in=in+1 3415 if m3=3 then if m2=2 then z=z+2: k2: mauf 3420 if m3=3 then if m2=3 then z=z+2: k3: mauf 3425 end proc 3600 proc mauf 3610 z=z-4: k5: f%(j,i-1)=5: f%(j,i)=g%(j,i) 3620 end proc
Ist an M3 ein Parkett (ID 2), läuft es so ab: In Z. 3410 wird am Standort (M2) ein Parkett ausgegeben (k2). Danach wird in M3 die Kiste gezeichnet (PROC mauf) und im Array vermerkt, wo sie sich nun befindet (Z. 3610). Dann wird PROC pauf verlassen und in Z. 3240 der Sokoban an der Stelle eingetragen, wo eben die Kiste stand. Endzustand: Die Kiste steht in M3, der Sokoban in M1 und ein Parkett erscheint in M2.
Sollte der Sokoban auf einer Ablagefläche gestanden haben (ID 3 an M2), dann tritt die zweite Bedingung in Z. 3410 in Kraft und rekonstruiert in M2 die Ablagekachel (k3).
Wenn aber an M3 ein Ablagefeld ist (Z. 3415/3420), haben wir die Situation, dass der Sokoban zusammen mit einer Kiste die Ablage betritt. Eine Kiste ist danach in der Ablage. Dieses Ereignis muss registriert werden (in Z. 3412 wird es in Variable IN gezählt). Das Programm zählt also, wie oft eine Kiste erstmalig auf eine Ablagefläche geschoben wird.
War in M3 ein Hindernis, tritt wiederum Z. 3240 in Kraft. Scheinbar passiert dann nichts.
Die anderen drei Richtungen werden entsprechend behandelt (PROC pab, PROC pnr und PROC pnl).
Erfolgskontrolle
Ob die Ablage bereits voll ist, checken wir (abhängig von IN) in 3955. Der Zähler IN zählt so lange, bis er die Anzahl der vorhandenen Kisten erreicht hat. Ist das der Fall, wird in PROC ablage überprüft, ob alle diese Kisten immer noch in der Ablage stehen.
3700 proc ablage
3705 bflash 30,6,12
3710 colour,fs: print at(0,0)"";: centre" ARE YOU FINISHED? "
3720 al=0: for i=1 to h: for j=1 to b
3730 x=g%(j,i): if x=3 then x=x+f%(j,i): if x=8 then al=al+1
3740 next: next: bflash off: colour,12
3760 print at(0,0) dup(" ",40) at(0,0)"";: centre"SOKOBAN"+str$(p)
3790 end proc
Dazu untersuchen wir alle Zellen des Klon-Arrays darauf, ob sie Ablagezellen sind (ID 3). Wird eine gefunden, addieren wir den Wert der gleichen Position im Spielfeld-Array (Z. 3730). Steht eine Kiste darauf (ID 5), ergibt sich der Wert 8. Dies bedeutet also, hier steht eine Kiste korrekt in der Ablage. Auch dieses Ereignis wird gezählt (in Variable AL). Entspricht AL der Anzahl der vorhandenen Kisten, ist das Ziel des Programms erreicht, alle Kisten stehen in der Ablage (al=pk in Z. 3965). Es gibt eine Erfolgsmeldung (in PROC finish).
Wenn nicht (die Addition ergibt dann nur den Wert 6 statt 8), stellen wir den Zähler IN (Betreten der Ablage) auf den Wert der in der Ablage gefundenen Kisten, damit korrekt weitergezählt werden kann (Z. 3955, zweite Bedingung). Das Spiel geht dann weiter.
Die Erfolgskontrolle kann also mehrmals aufgerufen werden. Da der Spieler an dieser Stelle eine kurze Zeit nichts tun kann, blinkt als Tätigkeitsanzeige währenddessen der Rahmen blau (Z. 3705) und im Kopf des Spielfelds erscheint ein Texthinweis.
Spiel-Ende
Ein erfolgreich abgeschlossenes Sokoban-Problem wird mit ein bisschen Bildschirm-Action "belohnt": Der Rahmen blinkt zwei Sekunden lang in grün (Z. 3820). Dann fragt das Programm, ob man ein neues Problem lösen möchte ("Next table?"). Bejaht man das, speichert es in Speicherstelle 2 die folgende Nummer (Z. 3860) und signalisiert mit x$="r", dass mit dieser nächsten Nummer neu gestartet werden soll (in Z. 3985).
3800 proc finish
3810 print at(0,0) dup(" ",36) at(0,0)"";: centre" YES, YOU MADE IT! "
3820 bflash 10,5,13: pause2: bflash off: colour,12
3825 x$="": loop: exit if place(x$,"xy")
3830 print at(0,0) dup(" ",36) at(0,0)"";: centre" NEXT TABLE? (Y/N) "
3840 fetch "yn",1,x$: if x$="n" then x$="x"
3845 end loop
3850 p=peek(2): if p=n then finale
3855 if x$="y" then p=p+1: x$="r"
3860 poke 2,p
3870 end proc
Sollte man bereits beim letzten der zehn Sokoban-Probleme angekommen sein, schreitet das Programm zum Finale (Z. 3850). Auch hier blinkt der Rahmen, diesmal 10 Sekunden lang (kann man mit der Return-Taste abkürzen). Am Ende jedoch wird der Bildschirm gelöscht, das Programm kehrt in den normalen Zeichensatz zurück und beendet das Spiel Sokoban (Z. 4570 und in der Folge Z. 110 bis 999).
4500 proc finale
4510 fill 0,0,40,25,224,fb: r$=dup(chr$($df),9): r$=inst(" ",r$,4)
4520 insert r$,7,10,20,11,12: print at(9,0)"";: centre"ALL FINISHED!"
4530 print at(lin+2,0)"";: centre"CONGRATULATIONS!"
4540 print at(lin+3,0)"";: centre"VISIT"
4550 print at(lin+1,0)"";: centre"MATHEMATIK.CH": colourfb,fb,fb
4560 bflash 30,fb,12: pause10: bflash off: colour,12
4570 x$="x": nrm: cls
4580 end proc
Erweiterungen einbinden
Das Spiel Sokoban kommt von Hause aus mit zehn oder elf zu lösenden Problemen, die auf das Original von Hiroyuki Imabayashi zurückgehen (die tatsächlichen Originale sind urheberrechtlich geschützt). Es gibt natürlich im Internet unendlich viele Sokoban-Problem-Seiten, sogar mit einer eigenen Notation, wie diese weitervermittelt werden können. Ein paar davon kann man auch im TSB-Sokoban ergänzen. Sie liegen auf Disk als "sokoban addon x" (x=laufende Nummer, ursprünglich 1 bis 4) mit jeweils zehn oder elf weiteren Problemen vor. Sie werden folgendermaßen eingebunden (nach Spielende oder vor Spielbeginn):
d! 6000-
merge "sokoban addon 1" (...2, 3 oder 4)
poke 2,0
run
Will man eigene Sokoban-Probleme vorgeben (die man z.B. hier finden kann), dann baut man einfach die DATAs so auf, wie sie in den Zeilen 6000 bis 6110 weiter oben zu sehen waren. Welche Kachel-IDs an welche Stelle gehören, hat man dabei schnell im Griff.
Eins noch zu den beiden Zeilen 3075 und 3112: Ein Spielfeld kann natürlich auch so geplant werden, dass bewegliche Objekte bereits beim Start auf Ablageflächen stehen. Also eine Kiste (Z. 3075) oder der Sokoban (Z. 3112) stehen auf einer Ablage. Damit das vom Programm erkannt werden kann, sind hierfür die IDs modifiziert: $88 für eine Kiste und 12 für den Sokoban. In Addon 2 kommen solche Sokoban-Felder vor.
Download Sokoban (ZIP-Datei eines D64, 30 KB)
Viel Spaß!
Sokoban 2.0
Seit Juni 2023 gibt es Sokoban 2.0. Die Knobelaufgaben sind darin die gleichen wie in 1.0, aber diese Version ist auf Geschwindigkeit getrimmt: Der Aufbau des Spielfeldes erfolgt innerhalb eines Augenblinzelns, eine wahre User-Wonne. Möglich wurde dies durch die Einführung des neuen Befehls MAP zur Darstellung von zeichensatzveränderten Spielfeldern auf dem Textbildschirm wie sie auch bei Sokoban als Grundlage dienen (s. oben).
Zur zusätzlichen Geschwindigkeitssteigerung wurden in 2.0 die Definitionen der Spielfelder in Nachladedateien ausgelagert, denn das Laden einer kleinen Datei ist wesentlich weniger zeitaufwändig als das sukzessive Befüllen eines Arrays mit diesen Informationen per DATA und READ wie in Version 1.0.
Im Unterschied zu Sokoban 1.0 können alle Knobelprobleme ohne Programmveränderung gespielt werden (kein MERGE mehr nötig). Die Level von Addon #3 und #4 (laufen in Version 2.0 unter dem Namen "biglevel", da sie den ganzen Bildschirm ausfüllen) aktiviert man mit einem POKE, bevor man das Spiel mit RUN startet (POKE $c647,1 - der Vorgabewert 0 an $c647 wählt die 10 Standard-Level und Addon #1 und #2 aus).
Weiterhin gilt der POKE-Tipp zur Auswahl eines bestimmten Knobelbildschirms per POKE 2, nummer bevor man RUN eingibt (mit PEEK (2) kann man die aktuelle Nummer herausfinden).
Und schließlich: In Version 2.0 ist von vornherein Joystickbedienung möglich, alternativ und parallel zur Tastaturbedienung.
Wir wünschen noch mehr Spaß mit Sokoban 2.0!